Mums svarbu išlaikyti jūsų privatumą. Dėl šios priežasties sukūrėme Privatumo politiką, kurioje aprašoma, kaip naudojame ir saugome jūsų informaciją. Peržiūrėkite mūsų privatumo praktiką ir praneškite mums, jei turite klausimų.

Asmeninės informacijos rinkimas ir naudojimas

Asmeninė informacija reiškia duomenis, kurie gali būti naudojami konkretaus asmens tapatybei nustatyti arba susisiekti su juo.

Jūsų gali būti paprašyta pateikti savo asmeninę informaciją bet kuriuo metu, kai susisiekiate su mumis.

Toliau pateikiami keli pavyzdžiai, kokios rūšies asmeninės informacijos galime rinkti ir kaip galime tokią informaciją naudoti.

Kokią asmeninę informaciją renkame:

• Kai pateikiate paraišką svetainėje, galime rinkti įvairią informaciją, įskaitant jūsų vardą, telefono numerį, adresą El. paštas ir tt

Kaip naudojame jūsų asmeninę informaciją:

• Mūsų surinkta Asmeninė informacija leidžia mums susisiekti su jumis ir informuoti apie unikalių pasiūlymų, akcijos ir kiti renginiai bei būsimi renginiai.
• Retkarčiais galime naudoti jūsų asmeninę informaciją svarbiems pranešimams ir pranešimams siųsti.
• Mes taip pat galime naudoti asmeninę informaciją vidiniais tikslais, tokiais kaip auditas, duomenų analizė ir įvairūs tyrimai siekdami pagerinti mūsų teikiamas paslaugas ir teikti rekomendacijas dėl mūsų paslaugų.
• Jei dalyvaujate prizų traukime, konkurse ar panašioje akcijoje, mes galime naudoti jūsų pateiktą informaciją tokioms programoms administruoti.

Informacijos atskleidimas trečiosioms šalims

Mes neatskleidžiame iš jūsų gautos informacijos trečiosioms šalims.

Išimtys:

• Esant poreikiui – įstatymų nustatyta tvarka, teismine tvarka, teismine tvarka ir (arba) remiantis viešais prašymais ar prašymais iš vyriausybines agentūras Rusijos Federacijos teritorijoje – atskleiskite savo asmeninę informaciją. Taip pat galime atskleisti informaciją apie jus, jei nuspręsime, kad toks atskleidimas yra būtinas arba tinkamas saugumo, teisėsaugos ar kitais visuomenei svarbiais tikslais.
• Reorganizavimo, susijungimo ar pardavimo atveju surinktą asmeninę informaciją galime perduoti atitinkamai trečiajai šaliai.

Asmeninės informacijos apsauga

Mes imamės atsargumo priemonių, įskaitant administracines, technines ir fizines, siekdami apsaugoti jūsų asmeninę informaciją nuo praradimo, vagystės ir netinkamo naudojimo, taip pat nuo neteisėtos prieigos, atskleidimo, pakeitimo ir sunaikinimo.

Jūsų privatumo gerbimas įmonės lygiu

Siekdami užtikrinti, kad jūsų asmeninė informacija būtų saugi, savo darbuotojams pranešame apie privatumo ir saugumo standartus ir griežtai vykdome privatumo praktiką.

Piramidės koncepcija

1 apibrėžimas

Geometrinė figūra, sudarytas iš daugiakampio ir taško, esančio ne plokštumoje, kurioje yra šis daugiakampis, sujungtas su visomis daugiakampio viršūnėmis, vadinamas piramide (1 pav.).

Daugiakampis, iš kurio padaryta piramidė, vadinamas piramidės pagrindu; susidarę trikampiai, sujungti su tašku, yra piramidės šoniniai paviršiai, trikampių kraštinės yra piramidės kraštinės, o taškas yra bendras. prie visų trikampių yra piramidės viršūnė.

Piramidžių rūšys

Priklausomai nuo kampų skaičiaus piramidės pagrinde, ji gali būti vadinama trikampiu, keturkampiu ir pan. (2 pav.).

2 pav.

Kitas piramidžių tipas yra taisyklingoji piramidė.

Įveskime ir įrodykime taisyklingos piramidės savybę.

1 teorema

Visi taisyklingos piramidės šoniniai paviršiai yra lygiašoniai trikampiai, kurie yra lygūs vienas kitam.

Įrodymas.

Apsvarstykite taisyklingą $n-$kampinę piramidę, kurios viršūnė $S$ aukštis $h=SO$. Aplink pagrindą nubrėžkime apskritimą (4 pav.).

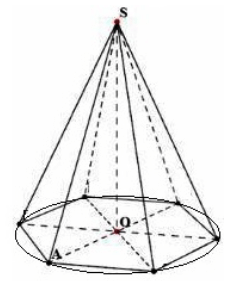
4 pav.

Apsvarstykite trikampį $SOA$. Pagal Pitagoro teoremą gauname

Akivaizdu, kad bet koks šoninis kraštas bus apibrėžtas tokiu būdu. Vadinasi, visi šoniniai kraštai yra lygūs vienas kitam, tai yra, visi šoniniai paviršiai yra lygiašoniai trikampiai. Įrodykime, kad jie vienas kitam lygūs. Kadangi pagrindas yra taisyklingas daugiakampis, visų šoninių paviršių pagrindai yra lygūs vienas kitam. Vadinasi, visi šoniniai paviršiai yra lygūs pagal III trikampių lygybės kriterijų.

Teorema įrodyta.

Dabar pristatysime tokį apibrėžimą, susijusį su taisyklingosios piramidės sąvoka.

3 apibrėžimas

Taisyklingos piramidės apotemas yra jos šoninio paviršiaus aukštis.

Akivaizdu, kad pagal Pirmąją teoremą visi apotemai yra lygūs vienas kitam.

2 teorema

Taisyklingos piramidės šoninio paviršiaus plotas nustatomas kaip pagrindo ir apotemos pusperimetro sandauga.

Įrodymas.

$n-$kampinės piramidės pagrindo kraštinę pažymėkime $a$, o apotemą - $d$. Todėl šoninio veido plotas lygus

Kadangi pagal 1 teoremą visos kraštinės yra lygios, tai

Teorema įrodyta.

Kitas piramidžių tipas yra nupjauta piramidė.

4 apibrėžimas

Jei per paprastą piramidę nubrėžta lygiagreti jos pagrindui plokštuma, tai tarp šios plokštumos ir pagrindo plokštumos susidariusi figūra vadinama nupjautąja piramide (5 pav.).

5 pav. Nupjauta piramidė

Nupjautinės piramidės šoniniai paviršiai yra trapecijos formos.

3 teorema

Taisyklingos nupjautinės piramidės šoninio paviršiaus plotas nustatomas kaip pagrindų ir apotemos pusperimetrų sumos sandauga.

Įrodymas.

$n-$kampinės piramidės pagrindų kraštines pažymėkime atitinkamai $a\ ir\ b$, o apotemą - $d$. Todėl šoninio veido plotas lygus

Kadangi visos pusės yra lygios, tada

Teorema įrodyta.

Pavyzdinė užduotis

1 pavyzdys

Raskite nupjautos trikampės piramidės šoninio paviršiaus plotą, jei jis gaunamas iš taisyklingos piramidės, kurios pagrindo kraštinė yra 4 ir apotema 5, nupjaunant plokštumą, einanti per šoninių paviršių vidurio liniją.

Sprendimas.

Pagal teoremą apie vidurio linija nustatome, kad sutrumpintos piramidės viršutinė bazė lygi $4\cdot \frac(1)(2)=2$, o apotemas lygus $5\cdot \frac(1)(2)=2.5$.

Tada pagal 3 teoremą gauname

Instrukcijos

Tuo atveju, jei bazėje piramidės yra kvadratas, žinomas jo įstrižainės ilgis, taip pat ir šio krašto ilgis piramidės, Tai aukščio tai piramidės galima išreikšti iš Pitagoro teoremos, nes trikampis, sudarytas iš briaunos piramidės, o pusė įstrižainės prie pagrindo yra stačiakampis.
Pitagoro teorema teigia, kad stačiakampio trikampio hipotenuzės kvadratas yra lygus jo kojų kvadratų sumai (a² = b² + c²). Kraštas piramidės- hipotenuzė, viena iš kojų yra pusė kvadrato įstrižainės. Tada nežinomos kojos ilgis (aukštis) randamas naudojant formules:
b² = a² - c²;
c² = a² – b².

Kad abi situacijos būtų kuo aiškesnės ir suprantamesnės, galite apsvarstyti porą.
1 pavyzdys: bazinis plotas piramidės 46 cm², tūris 120 cm³. Remiantis šiais duomenimis, aukštis piramidės yra taip:
h = 3*120/46 = 7,83 cm
Atsakymas: šio aukštis piramidės bus maždaug 7,83 cm
2 pavyzdys: U piramidės, kurio pagrindu yra daugiakampis - kvadratas, jo įstrižainė 14 cm, briaunos ilgis 15 cm Pagal šiuos duomenis rasti aukščio piramidės, turite naudoti šią formulę (kuri yra Pitagoro teoremos pasekmė):
h² = 15² - 14²
h² = 225–196 = 29
h = √29 cm
Atsakymas: šio aukštis piramidės yra √29 cm arba maždaug 5,4 cm

pastaba

Jei piramidės pagrinde yra kvadratas ar kitas taisyklingas daugiakampis, tai šią piramidę galima vadinti taisyklingąja. Tokia piramidė turi keletą savybių:
jo šoniniai šonkauliai yra vienodi;
jo paviršiai yra lygiašoniai trikampiai, kurie yra lygūs vienas kitam;
aplink tokią piramidę galima apibūdinti sferą, taip pat ją įrašyti.

Šaltiniai:

• Teisinga piramidė

Piramidė yra figūra, kurios pagrindas yra daugiakampis, o jos paviršiai yra trikampiai su bendra viršūne visiems. Tipiškose problemose dažnai reikia sukonstruoti ir nustatyti statmeną, nubrėžtą iš viršūnės piramidėsį jo pagrindo plokštumą. Šio segmento ilgis vadinamas aukščiu piramidės.

Jums reikės

• - valdovas
• - pieštukas
• - kompasas

Instrukcijos

Norėdami užbaigti, pastatykite piramidę pagal užduoties sąlygas. Pavyzdžiui, norint sukurti įprastą tetraedrą, reikia nupiešti figūrą, kad visos 6 briaunos būtų lygios viena kitai. Jei reikia statyti aukščio keturkampis, tada tik 4 pagrindo kraštai turi būti lygūs. Tada galite sukurti šoninių paviršių kraštus, nelygius daugiakampio kraštams. Pavadinkite piramidę, visas viršūnes pažymėdami lotyniškomis raidėmis. Pavyzdžiui, už piramidės su trikampiu prie pagrindo galite pasirinkti A, B, C (pagrindui), S (viršui). Jei sąlyga nurodo konkrečius briaunų matmenis, tada kurdami paveikslą vadovaukitės šiomis reikšmėmis.

Norėdami pradėti, sąlygiškai pasirinkite, naudodami kompasą, liestinę iš vidaus į visus daugiakampio kraštus. Jei piramidė, tada taškas (vadinkite jį, pavyzdžiui, H) ant pagrindo piramidės, į kurį nusileidžia aukštis, turi atitikti įbrėžto apskritimo centrą teisingas pagrindas piramidės. Centras atitiks tašką, esantį vienodu atstumu nuo bet kurio kito apskritimo taško. Jei sujungsite viršūnę piramidės S su apskritimo centru H, tada atkarpa SH bus aukštis piramidės. Atminkite, kad apskritimas gali būti įrašytas į keturkampį, kurio priešingų kraštinių suma yra vienoda. Tai taikoma kvadratui ir rombui. Šiuo atveju taškas H bus ant keturkampio. Bet kuriam trikampiui galima nubrėžti ir apibūdinti apskritimą.

Statyti aukščio piramidės, kompasu nubrėžkite apskritimą, o tada liniuote sujunkite jo centrą H su viršūne S. SH yra norimas aukštis. Jei bazėje piramidės SABC yra netaisyklinga figūra, tada aukštis sujungs viršūnę piramidės su apskritimo, į kurį įbrėžtas pagrindo daugiakampis, centru. Ant tokio apskritimo guli visos daugiakampio viršūnės. Šiuo atveju šis segmentas bus statmenas pagrindo plokštumai piramidės. Galite apibūdinti apskritimą aplink keturkampį, jei priešingų kampų suma yra 180°. Tada tokio apskritimo centras bus atitinkamo įstrižainių sankirtoje

Spręsdami uždavinį C2 koordinačių metodu, daugelis mokinių susiduria su ta pačia problema. Jie nemoka skaičiuoti taškų koordinatesįtraukta į skaliarinės sandaugos formulę. Iškyla didžiausi sunkumai piramidės. Ir jei baziniai taškai laikomi daugiau ar mažiau normaliais, tai viršūnės yra tikras pragaras.

Šiandien dirbsime ties įprasta keturkampe piramide. Taip pat yra trikampė piramidė (dar žinoma tetraedras). Tai sudėtingesnis dizainas, todėl jam bus skirta atskira pamoka.

Pirmiausia prisiminkime apibrėžimą:

Įprasta piramidė yra ta, kuri:

1. Pagrindas yra taisyklingas daugiakampis: trikampis, kvadratas ir kt.;
2. Aukštis, nubrėžtas į pagrindą, eina per jo centrą.

Visų pirma, keturkampės piramidės pagrindas yra kvadratas. Visai kaip Cheopsas, tik šiek tiek mažesnis.

Žemiau pateikiami piramidės, kurios visos briaunos lygios 1, skaičiavimai. Jei jūsų uždavinyje taip nėra, skaičiavimai nesikeičia – tiesiog skirsis skaičiai.

Keturkampės piramidės viršūnės

Taigi, tegul yra taisyklinga keturkampė piramidė SABCD, kur S yra viršūnė, o pagrindas ABCD yra kvadratas. Visos briaunos lygios 1. Reikia įvesti koordinačių sistemą ir rasti visų taškų koordinates. Mes turime:

Pristatome koordinačių sistemą, kurios pradžia yra taške A:

1. OX ašis nukreipta lygiagrečiai kraštinei AB;
2. OY ašis lygiagreti AD. Kadangi ABCD yra kvadratas, AB ⊥ AD;
3. Galiausiai nukreipiame OZ ašį aukštyn, statmenai ABCD plokštumai.

Dabar apskaičiuojame koordinates. Papildoma konstrukcija: SH – aukštis pritrauktas prie pagrindo. Patogumui piramidės pagrindą įdėsime į atskirą brėžinį. Kadangi taškai A, B, C ir D yra OXY plokštumoje, jų koordinatė yra z = 0. Turime:

1. A = (0; 0; 0) – sutampa su kilme;
2. B = (1; 0; 0) – žingsnis po 1 išilgai OX ašies nuo pradžios;
3. C = (1; 1; 0) - žingsnis po 1 išilgai OX ašies ir po 1 išilgai OY ašies;
4. D = (0; 1; 0) - žingsnis tik išilgai OY ašies.
5. H = (0,5; 0,5; 0) - kvadrato centras, atkarpos AC vidurys.

Belieka surasti taško S koordinates. Atkreipkite dėmesį, kad taškų S ir H koordinatės x ir y yra vienodos, nes jos yra tiesėje, lygiagrečioje OZ ašiai. Belieka rasti taško S z koordinatę.

Apsvarstykite trikampius ASH ir ABH:

1. AS = AB = 1 pagal sąlygą;
2. Kampas AHS = AHB = 90°, nes SH yra aukštis, o AH ⊥ HB kaip kvadrato įstrižainės;
3. Šoninė AH yra dažna.

Todėl stačiakampiai trikampiai ASH ir ABH lygus viena koja ir viena hipotenuzė. Tai reiškia, kad SH = BH = 0,5 BD. Bet BD yra kvadrato, kurio kraštinė yra 1, įstrižainė. Todėl turime:

Bendros taško S koordinatės:

Pabaigoje užrašome visų taisyklingos stačiakampės piramidės viršūnių koordinates:

Ką daryti, kai šonkauliai skiriasi

Ką daryti, jei piramidės šoniniai kraštai nėra lygūs pagrindo kraštams? Šiuo atveju apsvarstykite trikampį AHS:

Trikampis AHS - stačiakampis, o hipotenuzė AS taip pat yra originalios piramidės SABCD šoninis kraštas. Kojos AH nesunkiai apskaičiuojama: AH = 0,5 AC. Rasime likusią koją SH pagal Pitagoro teoremą. Tai bus taško S z koordinatė.

Užduotis. Duota taisyklinga keturkampė piramidė SABCD, kurios pagrinde yra kvadratas, kurio kraštinė 1. Šoninė briauna BS = 3. Raskite taško S koordinates.

Jau žinome šio taško x ir y koordinates: x = y = 0,5. Tai išplaukia iš dviejų faktų:

1. Taško S projekcija į OXY plokštumą yra taškas H;
2. Tuo pačiu metu taškas H yra kvadrato ABCD, kurio visos kraštinės lygios 1, centras.

Belieka rasti taško S koordinatę. Apsvarstykite trikampį AHS. Jis yra stačiakampis, su hipotenuze AS = BS = 3, o kojelė AH yra pusė įstrižainės. Norėdami atlikti tolesnius skaičiavimus, mums reikia jo ilgio:

Pitagoro teorema trikampiui AHS: AH 2 + SH 2 = AS 2. Mes turime:

Taigi taško S koordinatės:

Panašūs straipsniai